50-Years of Black-Scholes: Nobel Victory, Options Revolution

C=S N(d1​) − Ke−rt N(d2​)

In the annals of financial history, few accolades hold as much prestige and recognition as the Nobel Prize.  Such is the case with the Black-Scholes options pricing model, which achieved the remarkable feat in 1997 thanks to the persistence of a select group of professionals who saw its potential and heralded its practical application for over two decades, steadily infiltrating the innerworkings of financial institutions until it became an indispensable tool for options traders, risk managers and investors alike. Propelled into notoriety by the distinguished honor, the award cemented its status as a transformative force in the field of financial economics.

It was 50 years ago this month that Black-Scholes-Merton published their paper on pricing options which revolutionized the way derivatives are priced.

Their work simplified assets such as shares and futures into having a lognormal distribution and allowed pricing of options.

The Bank of International Settlements has reported as of the end of 2022, there were a total of $55.846 trillion option contracts outstanding across interest rates, currencies, commodities, and equities. This volume is attributed at least in part to the work started in 1973 by these rockstar quants.

The foreign exchange markets still use the Black-Scholes model for vanilla options and do a better job than the other asset classes at adapting the model. Black-Scholes has been described as ‘the wrong model with the wrong volatility to arrive at the right price.’

The model’s influence remains palpable, with countless researchers building on its foundations. It sparked a relentless pursuit of deeper understanding and more accurate valuation methodologies, leading to more sophisticated models that better capture the complexities of real-world financial markets.  In this article, we explore some of the adjustments that are made to make this model work.

Applying the Model to FX Markets

While the Black-Scholes model brought significant advancements to the field of finance, it is not without its limitations. Unlike the equity market where only certain expiries are quoted based on the futures dates, the FX market is over the counter. This means that any date and strike can be quoted giving a high degree of customization. The volatility input of the model forms a complex three-dimensional surface.

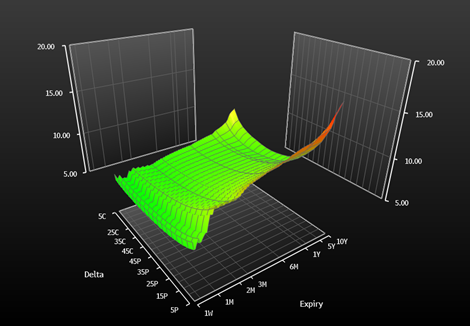
Volatility surface for EUR/JPY – Source Bloomberg

When applying the Black-Scholes options pricing model to the foreign exchange (FX) market, several adjustments are necessary to account for the unique characteristics of currency options. Here are some examples:

The Volatility Smile

Each date has a carefully constructed volatility smile. The smile is made of two components.

• The Butterfly: The Black-Scholes world assumes constant volatility, but we know this is not true. To simply explain this, on a large market spot move, volatility will move higher and the larger the move, the higher volatility will trade. The butterfly adjusts the prices of out-the-money options.
• The Risk Reversal: The price of out-the-money puts and calls will not always be symmetrical. For example, risk currencies like EUR/JPY fall and as result the EUR puts will be more valuable and priced higher.

These two elements are combined with a model such as Spline to ensure a smooth surface. Traders take great care to ensure the prices they quote are in certain ratios to make their smile smooth and arbitrage free.

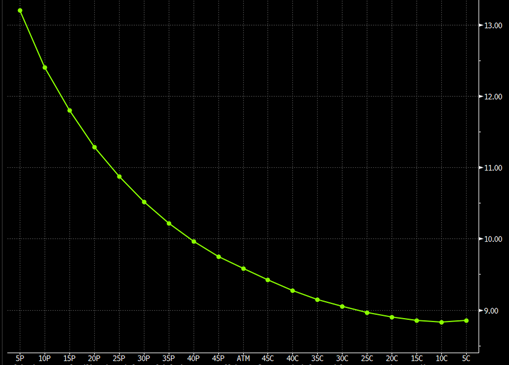
Volatility smile for 3-month EUR/JPY. Source Bloomberg

Date Adjustments

Each date has its own smile, but volatility is the element which is adjusted. Significant work needs to be done to ensure options are priced correctly and that the surface is free from arbitrage. Adjustments are made for weekends and holidays when the market is closed. Also, adjustments are made for key data releases and special events such as elections. To add to the complexity multiple cutoff times are thrown into the mix.

Greek Risks

The Black-Scholes model outputs Greeks risk to help manage portfolio risks (Delta/Gamma/Vega etc.). Unfortunately, these risks are not accurate enough to use in portfolio hedging as they do not account for the smile. Greeks can be calculated using simple bump and reprice models.

Exotic Options

The Black-Scholes model unfortunately cannot be used to price exotics as a single volatility assumption does not include the needed dynamics. It is, however, used by many traders as reference to ensure their adjustments are realistic.

Hedging Costs/Spreads

Academics often quote the model as ignoring transaction costs. This is not such a problem in practice as the interbank market quotes a 2-way volatility. This price spread is then applied to all strikes.

An Enduring Legacy

The principles of the Black-Sholes model continue to shape the financial industry today, in part because it is extremely fast to calculate. The inputs of spot, interest rates and volatility are all inputs to the model. The heavy lifting is all in calculating the correct volatility for the model.

With unsophisticated elegance, the Black-Scholes model brought forth a framework that effectively captured the essence of uncertainty inherent in financial markets, revolutionizing the way options are traded and managed and paving the way for advancements in derivative pricing.

This document is for information purposes only and does not constitute any recommendation or solicitation to any person to enter into any transaction or adopt any trading strategy, nor does it constitute any prediction of likely future movements in exchange rates or prices or any representation that any such future movements will not exceed those shown on any illustration. All exchange rates and figures appearing are for illustrative purposes only. You are advised to make your own independent judgment with respect to any matter contained herein.